机器学习
1. 机器学习算法
1.1 监督学习 (Supervised Learning)
Learns from data labeled with the “right answers”
将输入(input)x 映射到输出(output)y,从给定的正确答案中学习。
- 回归算法 (regression):预测房屋尺寸和房价的关系
- 分类算法 (classification):判断良性/恶性肿瘤
1.2 无监督学习 (Unsupervised Learning)
Find something interesting in unlabeled data
- 聚类算法 (clustering algorithm): Google news、DNA 微阵列数据
- 异常检测 (Anomaly detection):找到异常数据
- 降维 (Dimensionality reduction):压缩数据得到更小的数据集
1.3 Jupyter Notebook
# pip 安装
pip install jupyterlab
# 启动
jupyter-lab
2. 线性回归(linear regression)
2.1 一些定义
在机器学习中
$\hat{y}$表示对$y$的预测$f$函数称为模型$x$成为输入或者输入特征
2.2 如何表示 $f$
用线性函数 $f(x) = wx +b$ 表示,这样简单易用。并且以此作为基础,可以帮助获得更复杂的非线性模型。
2.3 代价函数(Cost Function)
有了函数之后,现在的问题变成了:找到合适的 $w$ 和 $b$,以便于更好的贴合训练集的真实数据。
我们创建一个代价函数(Cost Function)来衡量一条线与训练数据的拟合程度
构建出一个 $J(w,b)=\frac{1}{2m} \sum_{i=1}^{m} (\hat{y}-y_{n})^{2} $的公式(求平均有 2 是出于好计算)
因为有平方,所以也被称为平方误差代价函数 (Squared error cost function)。
在机器学习中,不同的人会用不同的代价函数,但迄今为止,平方误差代价函数通常用于线性回归,并且会得到很好的结果。
2.4 理解代价函数
我们最终的目的,是找到 $J$ 最小值对应的参数 $w$ 和 $b$
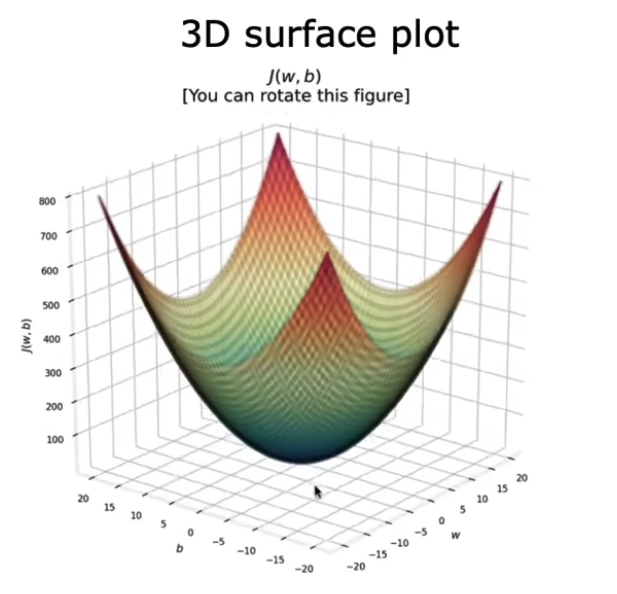
2.5 可视化代价函数
拥有$w$ 和 $b$两个参数的 $J$ 函数是一个三维的碗状图
3. 梯度下降(Gradient Descent)
梯度下降是一种算法,来尝试最小化任何函数
3.1 实现梯度下降
$\alpha $ 称为学习率(Learning rate),通常介于 0 和 1 之间。
$w$ 和 $b$ 的数据需要同时更新
$tmp\_w=w-\alpha \frac{\partial J(w,b )}{\partial w} $
$tmp\_b=b-\alpha \frac{\partial J(w,b )}{\partial b}$
$w=tmp\_w$
$b=tmp\_b$
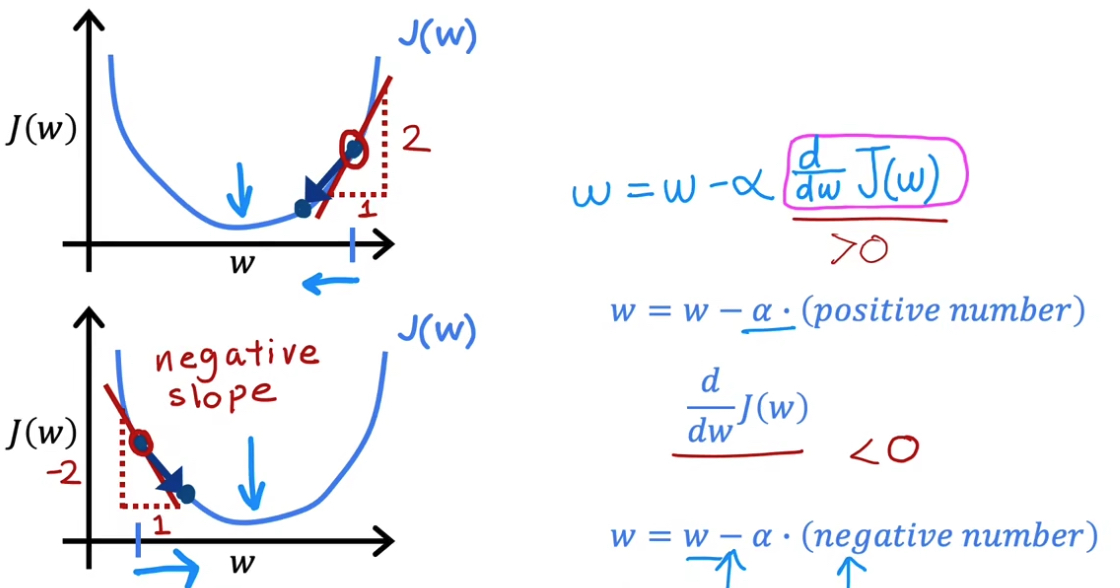
3.2 理解梯度下降
斜率为正数时,$w$ 减小向左移;斜率为负数时,$w$ 增加向右移。
3.3 学习率
学习率的选择至关重要。如果过小,会很慢;如果过大,可能会越过最小值,导致函数不能收敛甚至发散。
3.4 用于线性回归的梯度下降
将公式带入之后会得到:
$w = w - \alpha \frac{1}{m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}$
$b = b - \alpha \frac{1}{m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})$
3.5 运行梯度下降
更准确的说,这种梯度下降也被称为批量梯度下降(Batch gradient descent)。Batch 表示在进行梯度下降的每一步,都会用到 整个训练集。
4. 多维特征
对于上面 $f_{w,b}(x) = wx + b$ 这个单个特征模型来说,现实会有更多的维度。
具有 $n$ 个特征的模型会是如下的定义:
$f_{w,b}(x) = w_{1}x_{1}+w_{2}x_{2}+\dots +w_{n}x_{n}+b$。
我们不妨将它更简洁的表示:
$\vec{w}=\begin{bmatrix}w_{1} & w_{2} & w_{3} & \dots & w_{n}\end{bmatrix}$
$\vec{x}=\begin{bmatrix}x_{1} & x_{2} & x_{3} & \dots & x_{n}\end{bmatrix}$
$f_{\vec{w},b}(\vec{x})= \vec{w}\cdot \vec{x} + b$
这种具有多个输入特征的线性回归称为多元线性回归。为了方便实现,有一个很巧妙的技巧:矢量化。
4.1 矢量化
如果不用矢量,用程序实现 $f_{\vec{w},b}(\vec{x})= \sum_{i=1}^{n}w_{j}x_{j}+b$
f = 0
for j in range(0, n):
f = f + w[j] * x[j]
f = f + b
用矢量,即实现 $f_{\vec{w},b}(\vec{x})= \vec{w}\cdot \vec{x} + b$
import numpy as np
f = np.dot(w,x) + b
优点: 1. 代码编写简单 2. 运行效率高(Numpy 的 dot 函数能使用并行硬件的能力)
4.2 用于多元线性回归的梯度下降
$w_{n}=w_{n}-\alpha \frac{1}{m} \sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x} ^{(i)})-y^{(i)})x_{n} ^{(i)}$
$b=b-\alpha \frac{1}{m} \sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x} ^{(i)})-y^{(i)})$
4.3 特征缩放
目的提高效率。
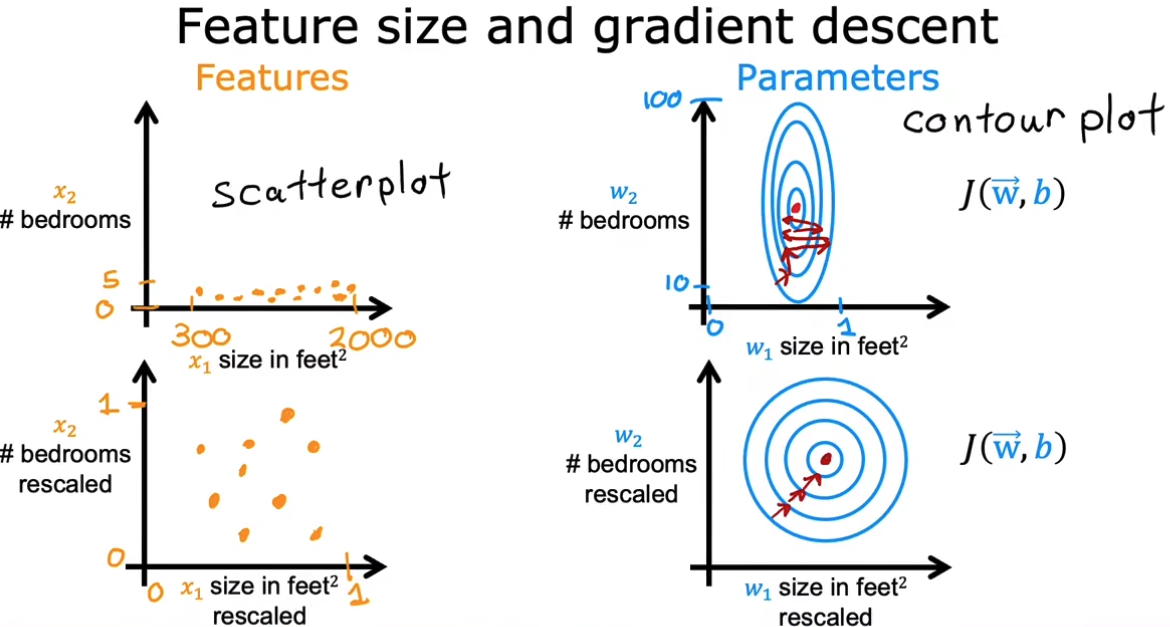
用图更直观的表示:当存在不同特征值时,取值范围不同,会导致梯度下降缓慢。但重新缩放不同特征,让它们处在可比较的范围内,速度和梯度的更新会显著提升。
4.4 如何实现特征缩放
- 均值归一化(Mean normalization)
- Z-score 标准化(Z-score normalization)
4.5 判断梯度下降是否收敛
梯度下降时,通过观察迭代次数 Iterations 和代价函数 $J(\vec{w},b)$ 所构建的 学习曲线。
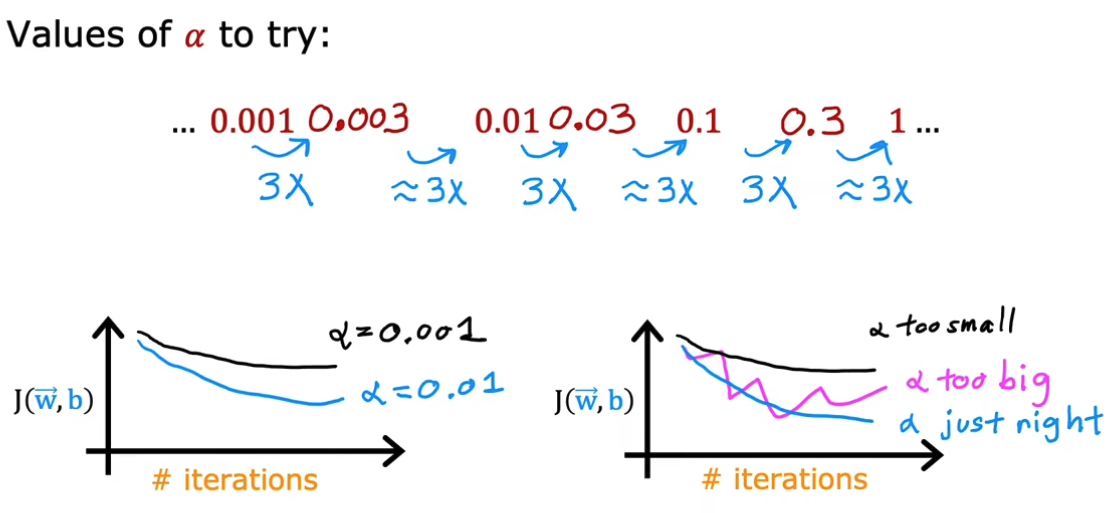
4.6 选择合适的学习率
过小的学习率会让迭代成本增加;过大则可能会导致发散。Andrew Ng 的习惯是用 3x 的策略去寻找并绘制合适的学习曲线。
4.7 特征工程(Feature engineering)
对于许多实际应用中,选择或输入正确的特征是使算法运行良好的关键步骤。
Feature engineering: Using intuition to design new features, by transforming or combining original features
有时候通过定义新特性,可以得到更好的模型。
4.8 多项式回归
相比直线而言,曲线更符合大多数情况。scikit-learn 是一个开源的机器学习库,可以把它用于你训练的模型中。
5. 逻辑回归
对于分类问题,线性回归最佳的拟合线不能解决问题。逻辑回归则用于解决输出标签 $y$ 是 0 或 1 的二元分类问题。
5.1 模型定义
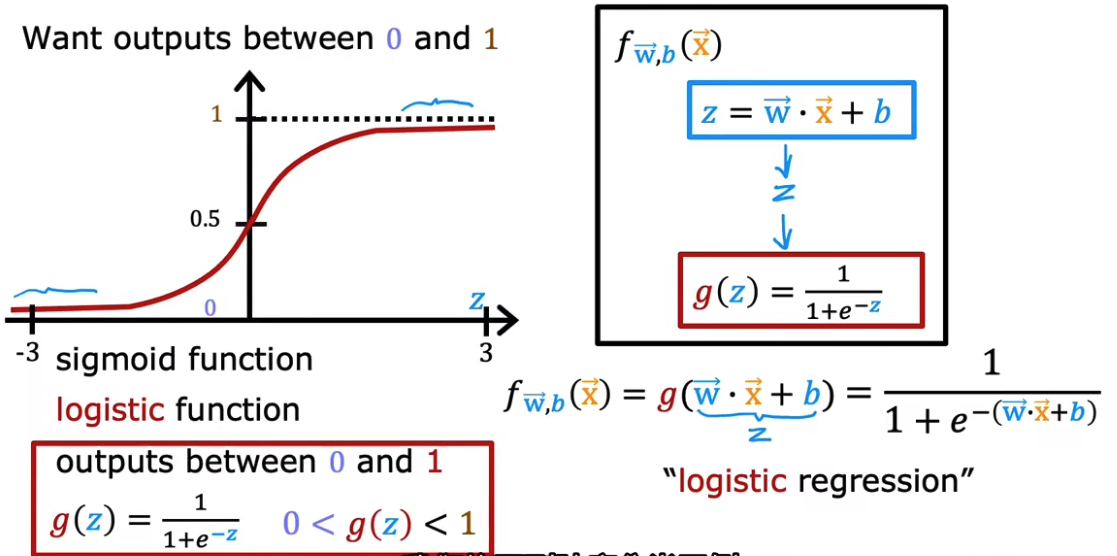
5.2 决策边界
- 线性决策边界
- 非线形决策边界
5.3 逻辑回归中的代价函数
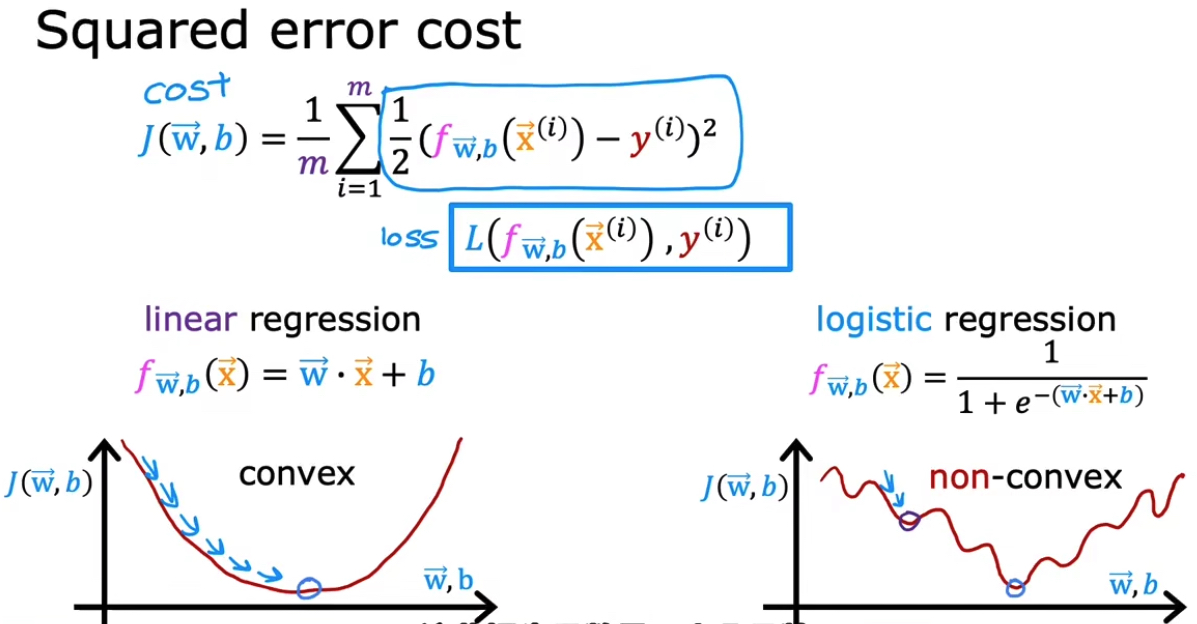
如果用线形回归的代价函数,套用到逻辑回归的代价函数中,会得到一个非凸函数,这样不适用于梯度下降。
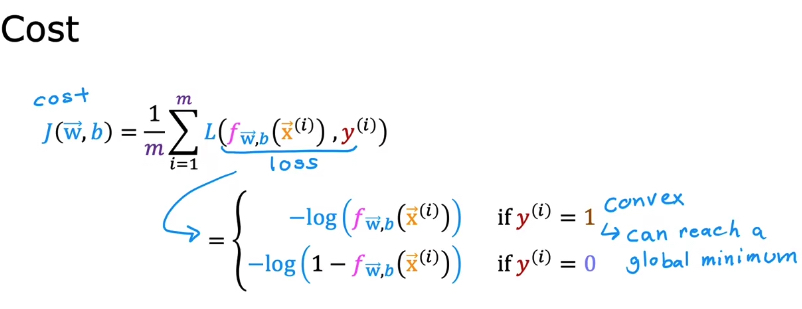
5.4 简化逻辑回归代价函数

5.5 实现梯度下降


6. 过拟合问题
线形回归过拟合
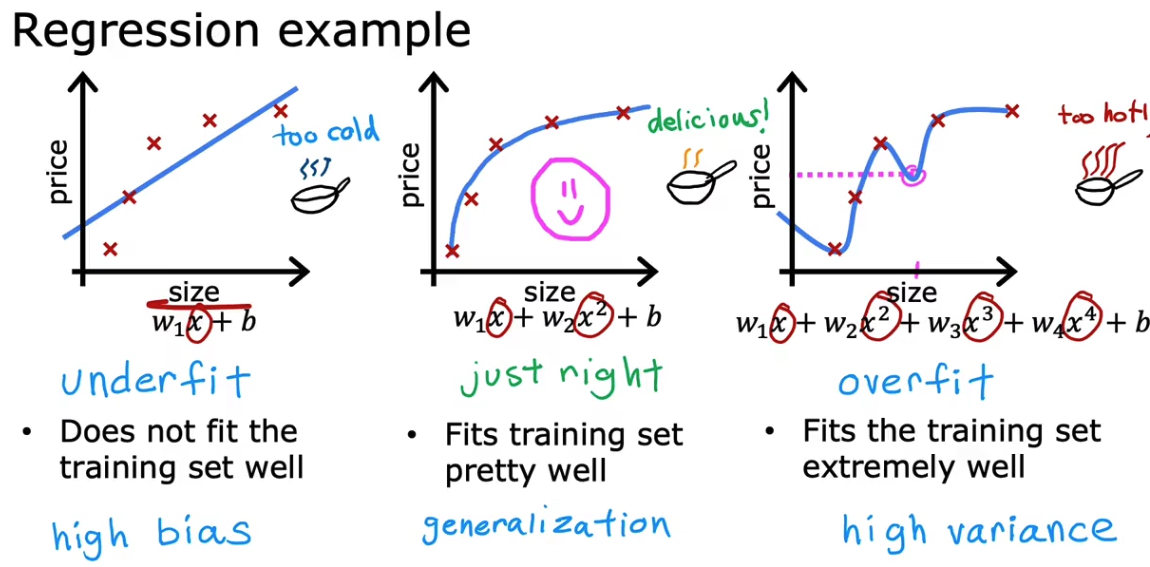
分类过拟合
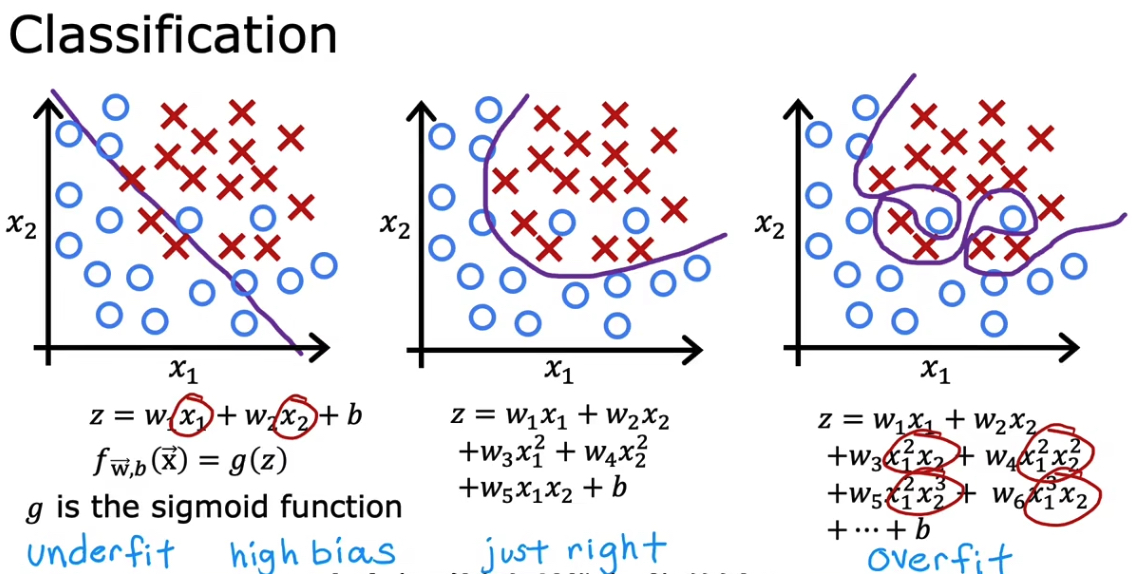
过于贴合训练集的数据,导致不能很好的泛化。
6.1 解决过拟合问题
- 收集更多的训练集(但并不总是会有很多的数据可供收集)
- 减少特征选项
- 正则化(温和减少特征,鼓励学习算法缩小参数)